Why are Quantum Computers a Thing?

In case you don't want to have to watch a million explanatory videos with perplexing math equations, let me give you the simple version.

Oct 30, 2025

If you’re like me and you watched The 3-Body Problem, you might be hoping that quantum computers can contain advanced communication equipment that allows for people to send information instantaneously over huge, interstellar distances.

Nope. Sorry to disappoint you. They absolutely can’t do this. (I spoke to a real human physicist about this, who also happens to be my dad). That’s not a thing, because that’s not how quantum entanglement works.

Yet, people are still wildly excited. So what gives? What’s so special, here?

It’s about how these computers hold and process data.

Let’s back up for a second and talk about Shrödinger’s cat, one of the most common paradigms for thinking about quantum states. I think I can assume that most people have heard about this one, but let me know if you haven’t. The way Shrödinger explained quantum states goes kinda like this: You put a cat into a box with some poison and close the lid. When you open the box, the cat either triggered the poison to release and it died, or it didn’t trigger the poison to release and is alive. It’s either alive or dead when you OPEN the box: but until you open it, it exists in a state of superposition: it’s simultaneously both alive and dead. I don’t know what this guy had against cats, but I guess it’s memorable.

I made you a drawing to illustrate the Shrödinger paradigm. For this article, please note that I’ve shifted the analogy: the “skeleton kitty” isn’t dead, but is simply wearing a Halloween costume. No real or theoretical cats were harmed in the making of this illustration series ;)

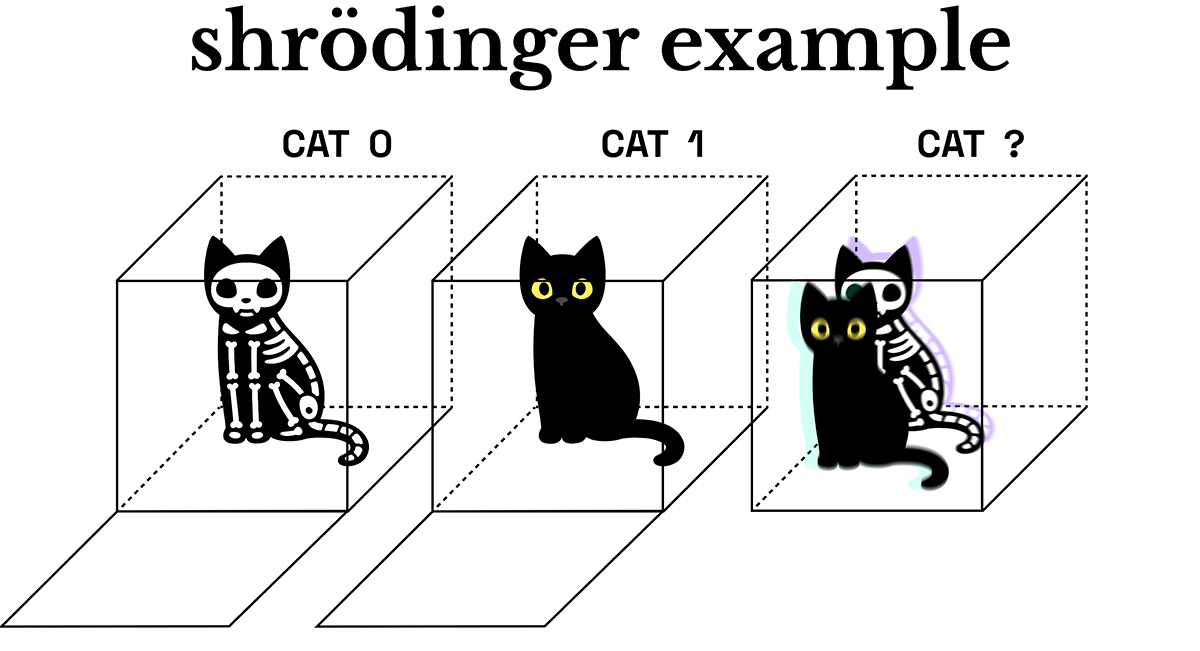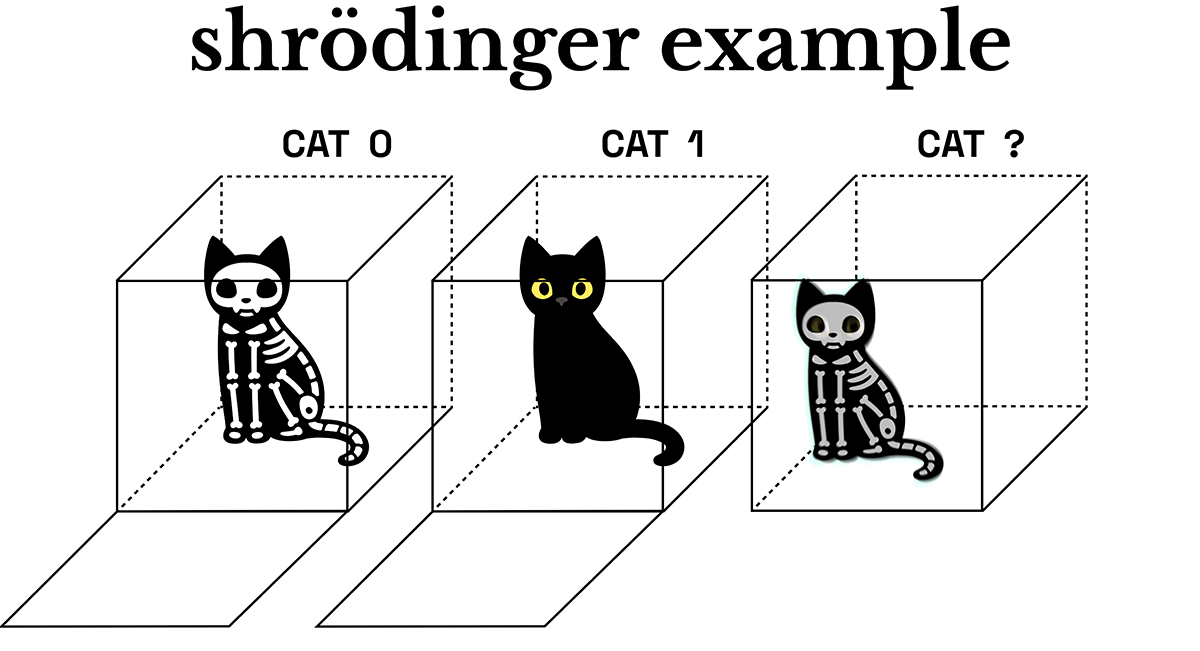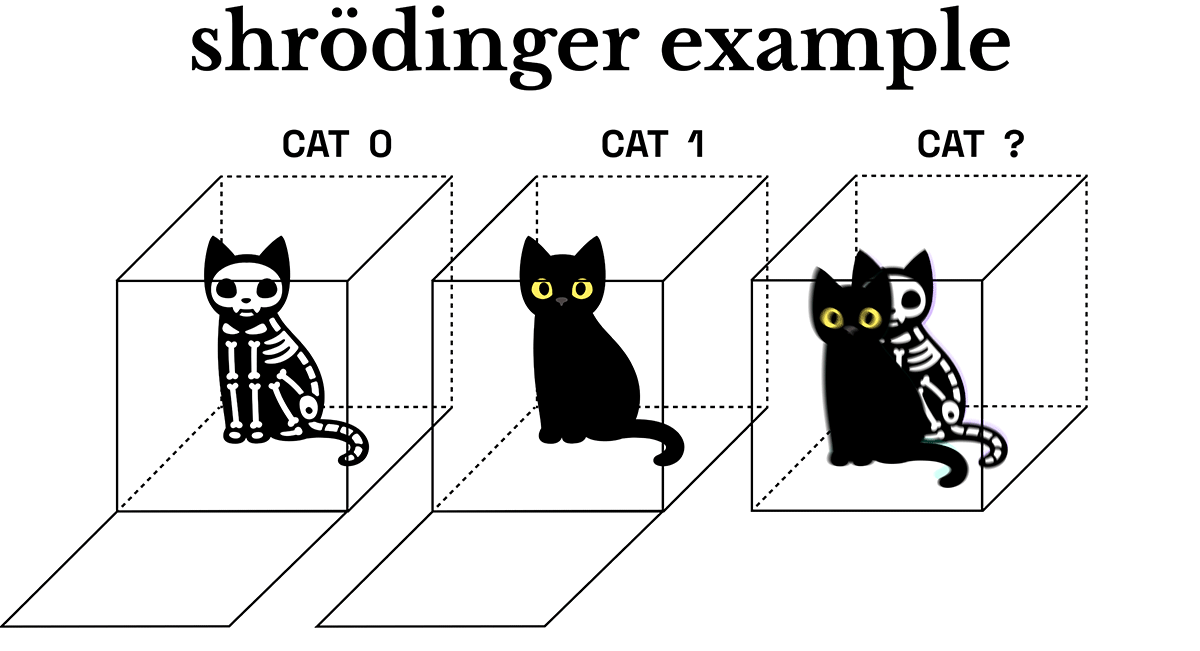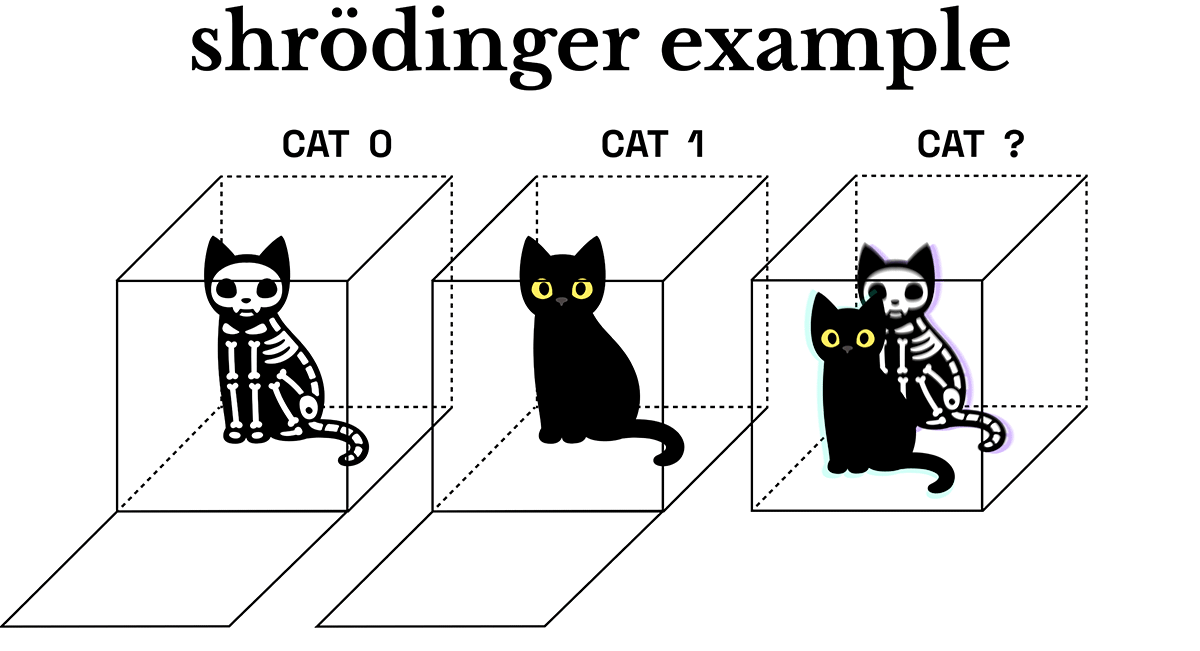
Until the box is opened, the regular and costumed version of the cat exist in a state of superposition.

It’s important to note here that not only do we not know the state of the cat, but the cat is actually both costumed and normal - simultaneously. The act of opening the box collapses the quantum state - and we either get Skelly Kitty or Normal Kitty.

Anyways, back to computers.

Standard Computers

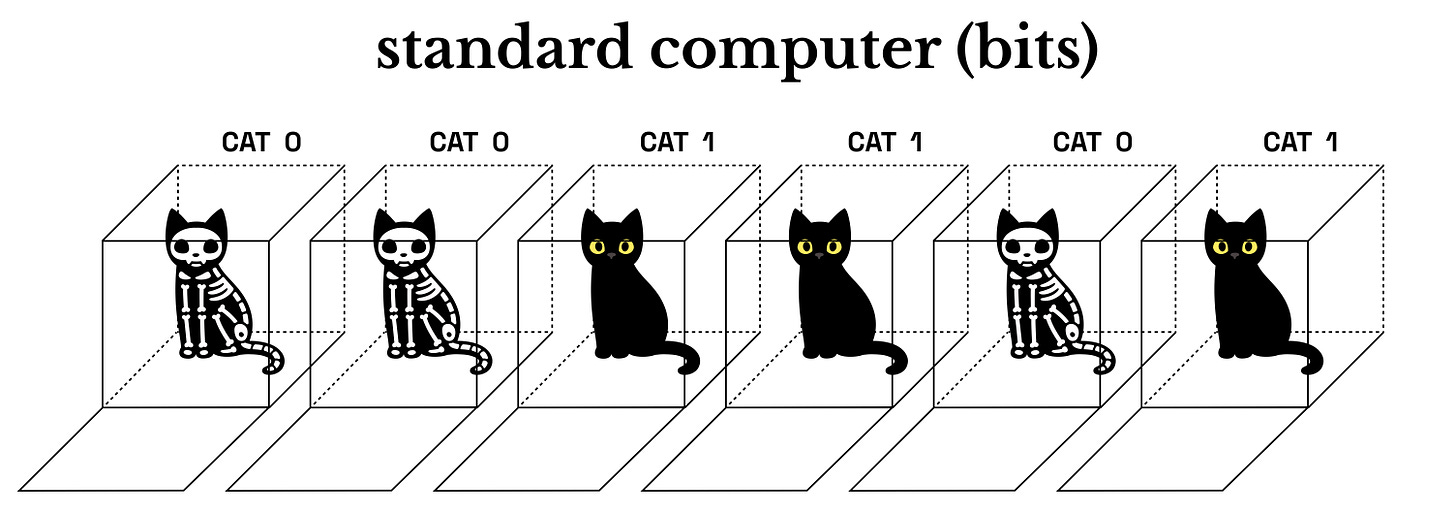
The most basic unit of information in a standard computer is called a bit. A bit is either “on” or “off”; it’s either “0” or “1”. If you put 8 bits together, you get a byte, which together can represent a letter, number or color. Put enough bytes together (~1 trillion or so) and you get enough to contain a hard drive’s worth of information (1TB). Standards computers use transistors on silicon chips. This structure means that regular computers have a very linear way of solving problems - more on that later.

A standard computer (or in this case, a CATputer) is comprised of units of 0s and 1s.

Quantum Computers

In contrast, the most basic unit of information in a quantum computer is called a qubit. A qubit can be either 0, 1 - or in a superposition state of both simultaneously! (Hot dog!…I mean cat.) A quantum computer uses superconducting circuits, trapped ions, or other systems which often need to be cooled to close to absolute zero to maintain quantum states.

While it entertains me endlessly to imagine that computers are filled with tiny quantum cats, it is here I should note that this is an imperfect analogy to describe how a qubit works. I’ll follow at the end with a list of resources to explore further. All you need to know for now is that we don’t know what state the qubits are in until the computer solves the problem and provides an output, kind of like this:

| 011110 >

Where the value of this particular output is a string of binary sandwiched in between a “|” and a “>”. This type of notation is called a ket and it indicates when an output has been provided through a quantum computation. The output appears randomly (yes, randomly!) based on the probabilities attached to all possible answers. Physicists and engineers are able to manipulate the probable outputs such that the right answer is more likely to appear, using certain algorithms, eg Grover’s Algorithm or the Hadamard Gate. But enough on that for now. Let’s move on to discuss how standard computers and quantum computers differ in their approach to problem-solving.

The Difference Between How Standard Computers and Quantum Computers Solve Problems

Standard computers tackle problems iteratively - meaning that they explore solutions one at a time. However, because quantum computers have a fundamentally different basis, they are able to explore all possible solution paths at the same time. How could this possibly be, you ask? One of my favorite visualizations for this comes from a video by Lukas’s Lab and it goes like this:

Imagine you’re trying to solve a maze. A standard computer will solve the maze in the way you’d expect: picking a direction, and changing direction if that direction doesn’t work. Although there are clever ways to speed this up, the standard computer is limited to exploring options one at a time.

Solving a maze the “standard computer” way

Now imagine you could flood the maze with water - as the water fills up the maze, the current flows in the direction of the way “out”. There’s only one solution, and it guides you there. In a sense, the water, similar to a quantum computer, has explored all possible paths simultaneously and chosen the “correct” one.

Solving a maze the “quantum computer” way

This analogy is also imperfect, because it gives the impression that you’re guaranteed to find the right answer, which is not the case. Remember what I said before: the output appears randomly based on the probabilities attached to all possible answers! So currently, this one of the problems physicists are working on solving; how to get the answers to be be more reliable. For example, IBM’s quantum computers often rerun algorithms over 1,000 times - and go with the answer that appears most frequently, in order to produce more reliable results.

So why do we care?

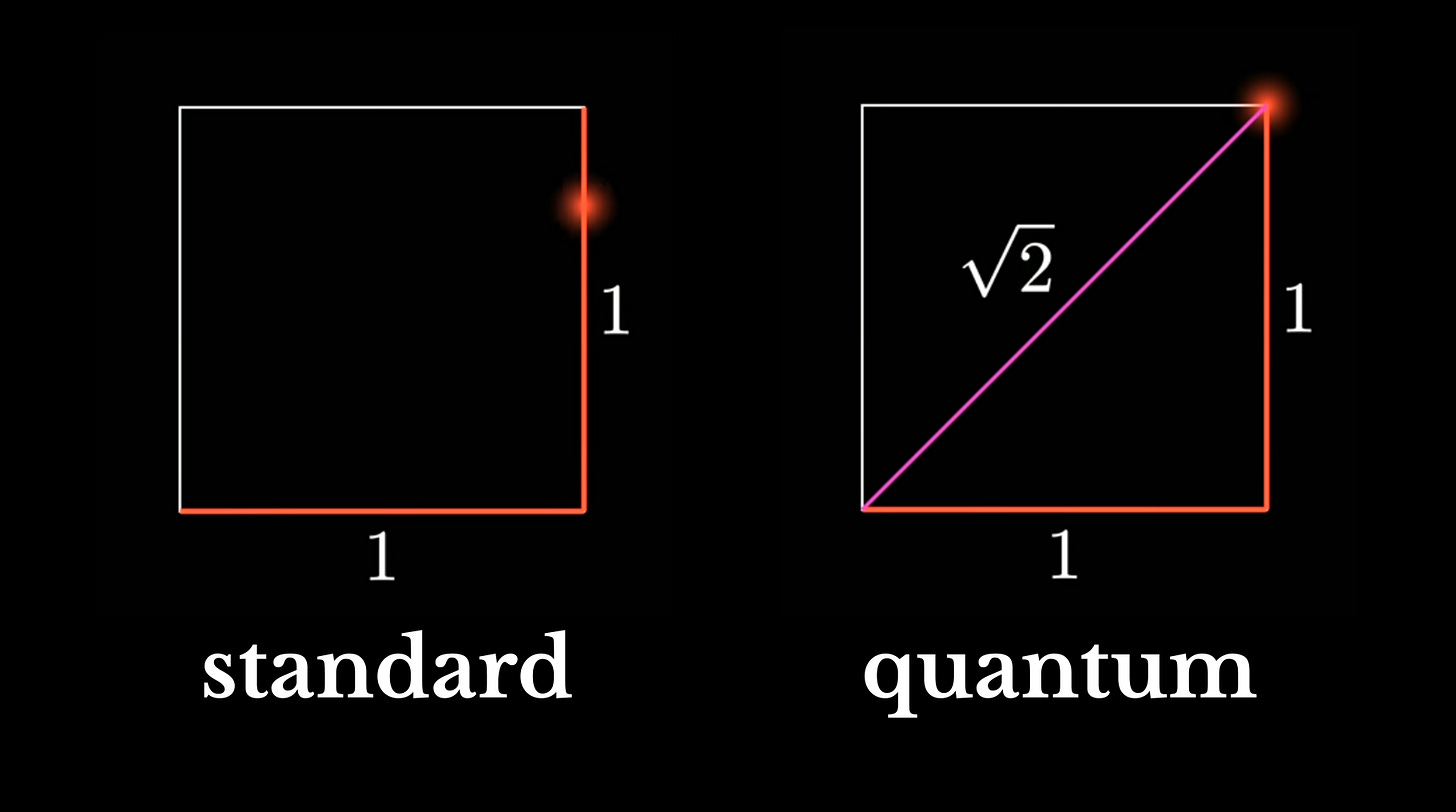
We’re back at last to the question that started this: why do we care about qubits and quantum computers? Well, they have the potentially to enormously speed up calculations of REALLY difficult problems - things that would take a standard computers years to complete, if at all. Don’t get TOO excited - it doesn’t actually make sense to use a quantum computer for most of the tasks you’re doing on a typical basis. But, let’s try to qualify (in a really simple way) WHY there’s a speed up at all. Rather than thinking of it as being an advantage of parallel processing, it’s more about the fact that you can save time if you aren’t limited to having to explore one option at a time. For example, if you’re trying to traverse a 1x1m square and you are limited to walk only perpendicular routes, the distance to your destination will be 2m. But if you can walk diagonally, you can get there in √2m. 3Blue1Brown’s video summarizes it visually like this, which is super helpful: